

Matrices (행렬이란?)
- 자연수 m,n∈N 에 대해, 실수값을 갖는 (m,n) 행렬 A는 요소 aij로 구성된 mxn 순서쌍
- i = 1...m, j = 1...n, m개의 행과 n개의 열로 이루어진 직사각형 배열

- (1, n)-matrices는 row라고 하고, (m,1)-matrices는 column이라고 한다.

Matrix Addition and Multiplication (행렬의 덧셈과 곱셈)
- 덧셈:
각 위치에 맞는 원소를 더하면 된다.

- 곱셈:
행렬 A∈(R)m×n, $B \in \mathbb(R)^{n \times k}$
에 대해 원소 cij 의 곱셈 C=AB∈(R)m×k 는 다음과 같이 계산된다.

즉, cij 는 A의 i번째 행과 B의 j번째 column에 속하는 원소를 곱하는것이다.

잘 알려져있듯이 행렬을 곱할때는 가운데 있는 차수가 같아야 곱셈이 가능하다.
★ 행렬의 곱셈은 교환법칙 성립 안함. (Example 2.3 참고) ★
Hadamard Product
- 행렬의 곱셈은 동일한 위치에 있는 원소의 곱이 아니다. (cij≠aijbij)
- 요소별 곱셈은 Hadamard 곱이라고 부른다.
Example 2.3

Identity Matrix (항등 행렬)
- 다음과 같이 n x n (정사각) 행렬이면서 대각 성분이 모두 1이고 나머지 원소는 모두 0인 행렬을 Identity Matrix라고 한다.

특징)
- 결합 법칙 성립:

- 분배 법칙 성립:
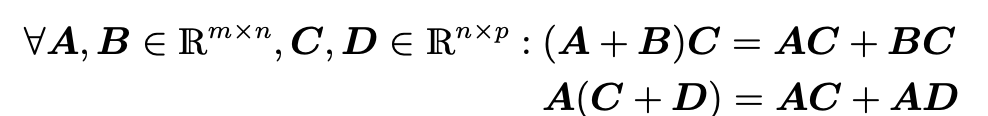
- 어떤 행렬에 Identity Matrix를 곱하면 자기자신이 나온다.
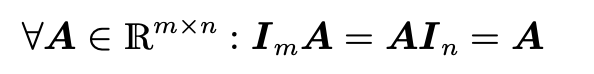
Inverse Matrix (역행렬)
- 정사각 행렬 A∈(R)n×n 에 대해 B∈(R)n×n가 AB=In=BA를 만족하면 B는 A의 역행렬이다.
- 역행렬이 존재하는 행렬을 regular/invertible/non-singular 행렬이라고 부른다.
- 역행렬이 존재하지 않는 행렬을 singular/noninvertible 행렬이라고 부른다.
- 2x2 행렬의 역행렬 존재성
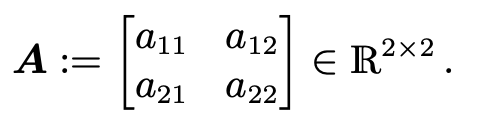
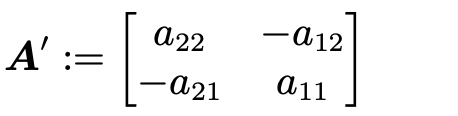
위 A 행렬에 대해 A'를 곱하면 다음과 같은 행렬을 얻음.
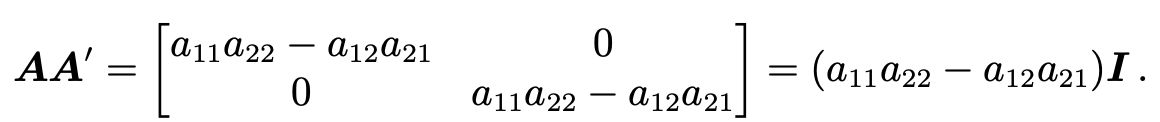
따라서, A의 역행렬을 다음과 같다.
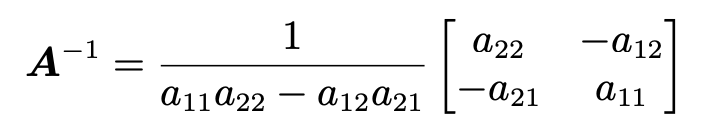
이때, 분모가 0이면 안되기 때문에 역행렬이 존재하기 위해서는 a11a22−a12a21≠0이여야 한다.
Example 2.4 (역행렬 예시)
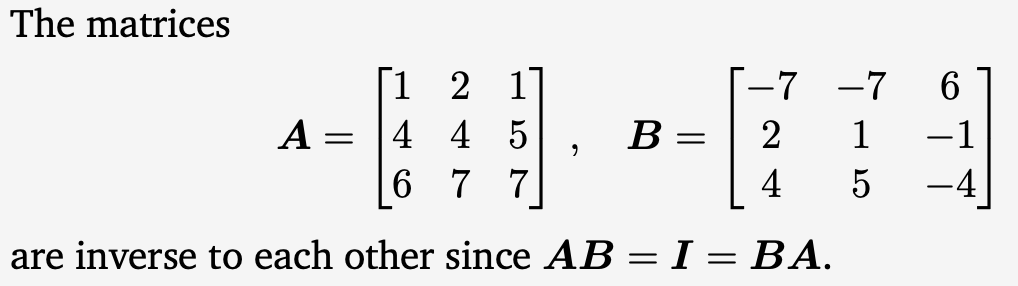
Transpose Matrix (전치행렬)
- A∈(R)m×n 행렬과 B∈(R)n×m 행렬에 대해 bij=aji 면 A의 transpose라고 부른다. (B=AT)
특징)
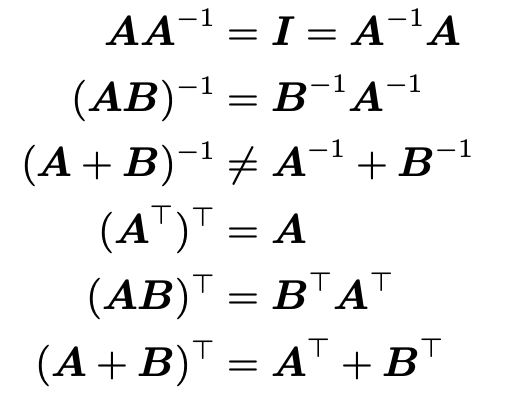
Symmetric Matrix (대칭 행렬)
- 만약 A=AT면 A를 대칭행렬이라고 한다.
특징)
- nxn 정사각 행렬만 대칭행렬이 될 수 있다.
- 만약 A의 역행렬이 존재하면, AT 또한 역행렬이 존재한다.
- ★ symmetric matrix의 덧셈은 항상 대칭행렬이 되지만, 곱셈은 그렇지 않다. ★
Multiplication by Scalar (스칼라배)
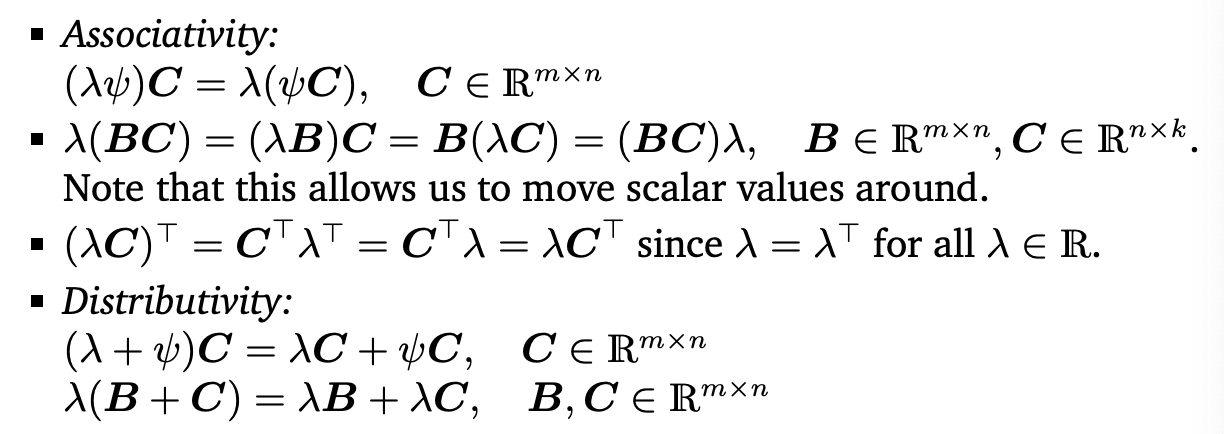
Example 2.5 (분배법칙 예시)
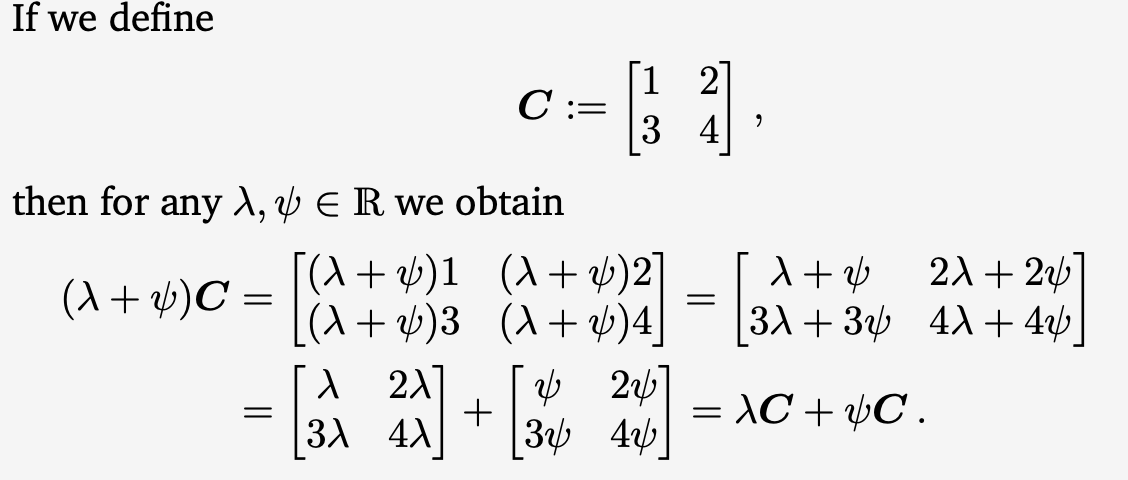
'전공 서적 읽기 > Mathematics for Machine Learning' 카테고리의 다른 글
| 2.6 Basis and Rank (0) | 2024.10.13 |
|---|---|
| 2.5 Linear Independence (0) | 2024.10.13 |
| 2.4 Vector Spaces (0) | 2024.10.12 |
| 2.3 Solving Systems of Linear Equations (1) | 2024.10.12 |
| 2.1 Systems of Linear Equations (0) | 2024.10.12 |

전공 공부 기록 📘
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!



