

선형방정식 풀기
- 선형방정식을 matrix multiplication (Ax = b 형식)으로 나타낼 수 있다.

Particular and General Solution
일반해 구하는 방법
1. Ax = b를 만족하는 particular solution을 찾는다.
2. Ax= 0 을 만족하는 모든 해를 찾는다.
3. 1번 방법과 2번 방법을 혼합해 일반해를 구한다.
기본행 연산
1. 두행을 교환한다.
2. 행을 상수배한다.
3. 서로 다른 두 행 더하기
이제 "일반해 구하는 방법"과 "기본행 연산"을 사용해 선형방정식의 일반해를 구해보자.
Example 2.6

첨가행렬을 만들어 가우스 소거법을 진행한다. (행 사다리꼴 row-echelon from 을 만든다.) 과정은 다음과 같다.

가우스 소거법을 한 행렬은 다음과 같다.

각 행의 첫번째 요소를 pivot이라 하고, pivot이 존재하는 열을 pivot column이라고 한다.
pivot column에 해당하는 x는 basic variable, non-pivot column에 해당하는 변수는 free variable이라고 한다.
해당 행렬에서는 가 free variable이다.

이제 일반해를 구하기 위해 step 1 ~ 3까지 진행해보자.
Step 1. Ax = b를 만족하는 particular solution을 찾는다.
특이해를 구하기 위해서 free variable에 0을 대입하면 된다.
그러면 다음과 같이 x1, x3, x4를 구할수있다.
참고로 마지막 행을 보면 a+1이 0이 아니면 식이 불능이 나오기 때문에 a = -1이여야 한다.

Step 2. Ax= 0 을 만족하는 모든 해를 찾는다.
위 방정식들을 Ax = 0 형태로 만들고, free variable인 x2와 x5의 조합으로 만든다.

Step 3. 1번 방법과 2번 방법을 혼합해 일반해를 구한다.
혼합하면 다음과 같은 일반해를 구할수있다.
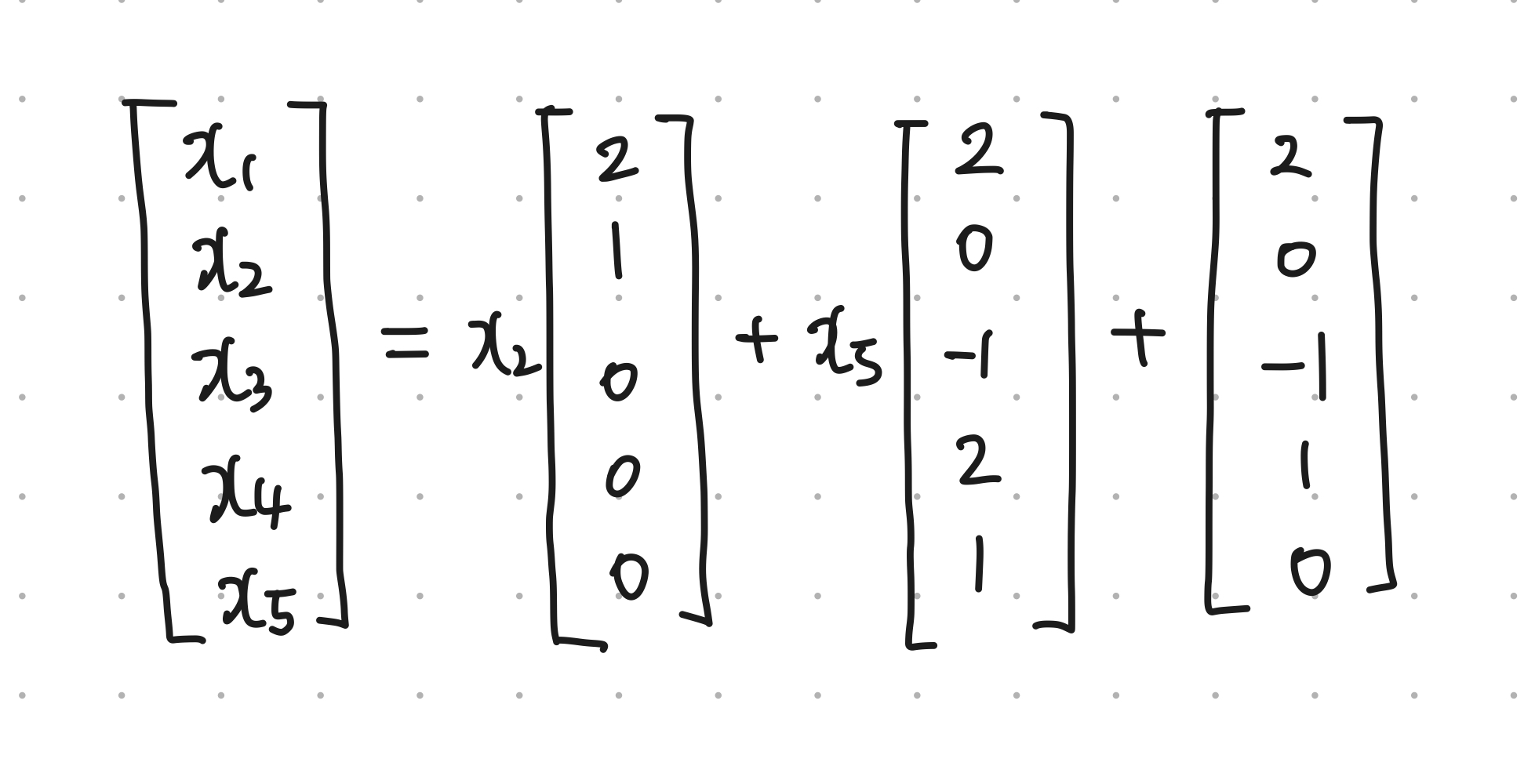
Step 1-3을 한번에 계산하는 방법은 다음과 같다.
x2와 x5로 식을 정리하고, x2의 계수 벡터 + x5의 계수 벡터 + 상수 벡터 까지 더해주면 한번에 일반해를 구할 수 있다.
풀이과정은 다음과 같다.

최종 답: x2, x5를 각각 람다1, 람다2로 변환
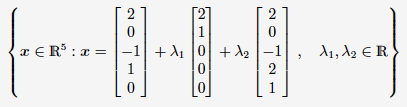
Row-Echelon Form (행사다리꼴)
행렬이 행-사다리꼴 형태에 있다고 할 때, 다음 조건들을 만족한다.
1) 오직 0으로만 이루어진 행들은 행렬의 맨 아래에 위치하며, 적어도 하나의 0이 아닌 원소를 포함하는 행돌은 0으로만 이루어진 행들 위에 위치한다.
2) 0이 아닌 행들만 고려했을때, 각 행에서 왼쪽에서 처음으로 나타나는 0이 아닌 숫자 (pivot)은 항상 그 위 행의 피벗보다 오른쪽에 있어야 함.
Reduced Row-Echelon Form
1) 행사다리꼴 형태여야 하고
2) pivot이 1이여야 한다.
3) pivot은 그 열에서 유일하게 0이 아닌값이다.
Gauss Elimination
선형 방정식을 기약행 사다리꼴 형태로 변환하기 위해 연산 수행하는 알고리즘
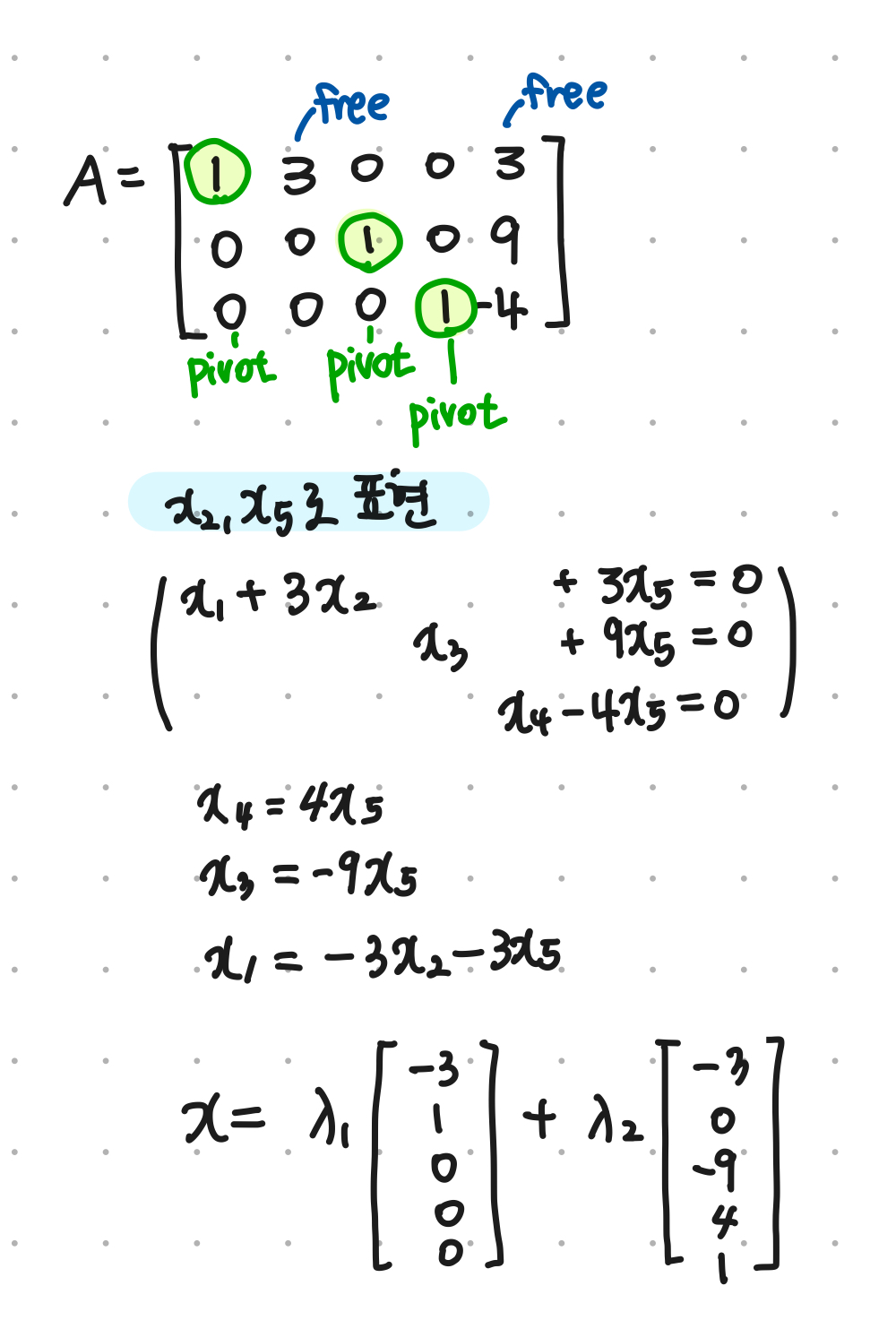
Example 2.7
'전공 서적 읽기 > Mathematics for Machine Learning' 카테고리의 다른 글
| 2.6 Basis and Rank (0) | 2024.10.13 |
|---|---|
| 2.5 Linear Independence (0) | 2024.10.13 |
| 2.4 Vector Spaces (0) | 2024.10.12 |
| 2.2 Matrices (0) | 2024.10.12 |
| 2.1 Systems of Linear Equations (0) | 2024.10.12 |

전공 공부 기록 📘
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!



